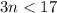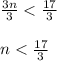Answer:

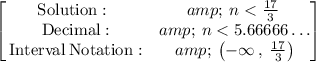
Explanation:
The question is an Algebra type of question. Before I learned Algebra, I usually just did as the question asked, I thought about what it meant. However, we can easily find the number "n" by following it in Algebraic terms.
Step 1: Set up an equation
"the sum of three times a number n and 8 is no more than 25"
Three times a number, "n"

The sum means addition, so;
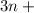
And 8. Combine;
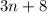
No more than 25, which means that both of them combined would still not result in something greater than 25, so it is less than 25.
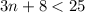
The Equation to solving the problem is
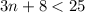 . Now we just have to solve it.
. Now we just have to solve it.
Step 2: Solve the equation
- Subtract 8 from both sides
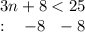
Plus 8 minus 8 cancels out. So we are left with 25-8 = 17.