Question

Consider the line y=7/4x-4.

Find the equation of the line that is perpendicular to this line and passes through the point (8,2)
Find the equation of the line that is parallel to this line and passes through the point (8,2)

Answer 1

`\displaystyle \perp\:y = -(4)/(7)x + 6(4)/(7) \\ \parallel\:y = 1(3)/(4)x - 12`

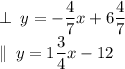
Step-by-step Step-by-step explanation:

Perpendicular equations have OPPOCITE MULTIPLICATIVE INVERCE RATE OF CHANGES [SLOPES], so 1¾ becomes −⁴⁄₇, and we move forward:

`\displaystyle 2 = -(4)/(7)[8] + b \hookrightarrow 2 = -4(4)/(7) + b; 6(4)/(7) = b \\ \\ \boxed{y = -(4)/(7)x + 6(4)/(7)}`

Parallel equations have SIMILAR RATE OF CHANGES [SLOPES], so 1¾ remains as is as we proceed:

`\displaystyle 2 = 1(3)/(4)[8] + b \hookrightarrow 2 = 14 + b; -12 = b \\ \\ \boxed{y = 1(3)/(4)x - 12}`

I am joyous to assist you at any time.