➤ Question:-
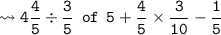

★ How to do :-
As we know that the BODMAS is the rule used here. It denates 'Brackets', 'Of', 'Division', 'Multiplication', 'Addition', 'Subtraction'. So, first we should do the brackets sums. But it's not given in this statement. Ao, first we should go for division, because of denotes multiplication which comes later. Then, we should multiply the fractions, then addition later on subtraction.

➤ Solution :-
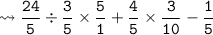

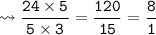
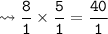
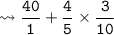
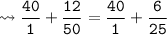
LCM of 1 and 25 is 25.

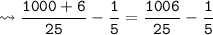
LCM of 25 and 5 is 25.
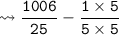
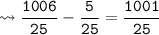

 The final answer of the sum is
The final answer of the sum is
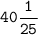 .
.
━━━━━━━━━━━━━━━━━━━━━━

BODMAS refers to
B denotes Brackets
O denotes 'OF' (Multiplication)
D denotes Division
M denotes Multiplication
A denotes Addition
S denotes Subtraction