Question

Please show steps and explain

Answer 1

`(n-6)/(3n) = (n-5)/(3n+1) \\\\(n-6)/(3n) - (n-5)/(3n+1) = 0\\\\((3n+1)(n-6)-3n(n-5))/(3n(3n+1)) = 0\\\\(3n+1)(n-6)-3n(n-5) = 0\\\\3n^2-18n+n-6-3n^2+15n=0\\\\3n^2-3n^2-18n+n+15n-6=0\\\\-2n-6=0\\\\2n+6=0\\\\2n=-6\\\\n=-3`

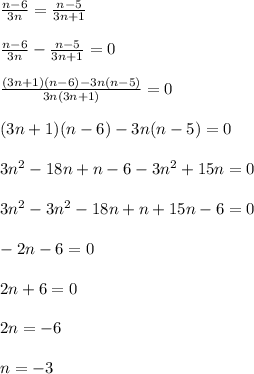
You can solve this equation by applying the zero product rule.

Firstly, you equate the expression to 0 in order to combine both fractions into one. As shown in Step 2, you find the LCM of both fractions and multiply accordingly. In this case, the LCM of both fractions is 3n(3n+1). Hence you cross multiply.

Next, you eliminate the denominator in order to solve the equation more conveniently. As you multiply the fraction by the denominator on the LHS, you do that to the RHS as well to maintain balance. 0×3n(3n+1)=0, hence Step 3.

Then, you expand the parentheses using the distributive law of multiplication, resulting in a quadratic equation.

Lastly, you solve the quadratic equation.

The answer is n=-3