Answer:
Choice B:
 .
.
Explanation:
For a parabola with vertex
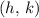 , the vertex form equation of that parabola in would be:
, the vertex form equation of that parabola in would be:
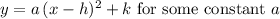 .
.
In this question, the vertex is
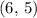 , such that
, such that
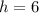 and
and
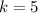 . There would exist a constant
. There would exist a constant
 such that the equation of this parabola would be:
such that the equation of this parabola would be:
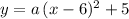 .
.
The next step is to find the value of the constant
 .
.
Given that this parabola includes the point
 ,
,
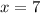 and
and
 would need to satisfy the equation of this parabola,
would need to satisfy the equation of this parabola,
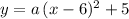 .
.
Substitute these two values into the equation for this parabola:
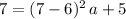 .
.
Solve this equation for
 :
:
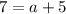 .
.
 .
.
Hence, the equation of this parabola would be:
 .
.