Question

The sum of the first 10 terms of a linear sequence is 5 and the sum

of the next 10 terms is 215. Find the sequence.

Answer 1

The first term of the sequence is -8.95 with a common difference of 2.1.

The sequence is:

-8.95, -6.85, -4.75, -2.65...

Explanation:

We are given that the sum of the first ten terms of a linear sequence is 5, and the sum of the next ten terms is 215.

And we want to find the sequence.

Recall that the sum of an A.P. is given by:

`\displaystyle S = (k)/(2)\left( a + x_k \right)`

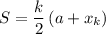
Where a is the first term, k is the number of terms, and x_k is the last term.

We can represent our term values with the direct formula:

`\displaystyle x_ n = a + d(n-1)`

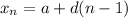
Where the first term, x₁ = a.

The sum of the first ten terms is 5. Hence, S = 5, k = 10, a = x₁ and x_k = x₁₀:
`\displaystyle\begin{aligned} \left( 5\right) &= (10)/(2) \left ( a + x_k\right) \\ \\ 5 &= 5\left( a + (a + 9d)) \\ \\ 2a + 9d &= 1 \end{aligned}`

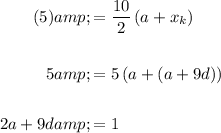
The sum of the next ten terms (that is, from x₁₁ to x₂₀) is 215. Hence, S = 215 when k = 10, a = x₁₁, and x_k = x₂₀:

`\displaystyle \begin{aligned} (215) &= ((10))/(2)\left( a + x_k\right) \\ \\ 215 &= 5\left((a + d(11-1))+(a+d(20-1))\right) \\ \\ 2a + 29d &= 43 \end{aligned}`

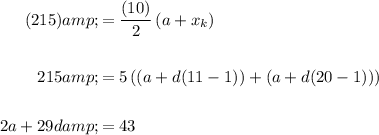
This yields a system of equations:

`\displaystyle \left\{ \begin{array}{l} 2a + 9d =1 \\ 2a + 29d = 43\end{array}`

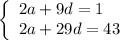
Solve:

`\displaystyle \begin{aligned} (2a +9d) + (-2a - 29d)& = (1) + (-43) \\ \\ -20d &= -42 \\ \\ d &= 2.1\end{aligned}`

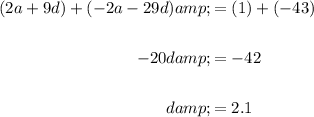
Consequently:

`\displaystyle \begin{aligned}a &= (1)/(2)\left( 1- 9d\right) \\ \\ &= (1)/(2)\left(1 - 9\left(2.1\right)\right) \\ \\&=-8.95 \end{aligned}`

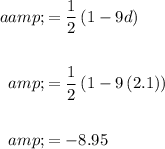
In conclusion, the first term of the sequence is -8.95 with a common difference of 2.1.

The sequence is:

-8.95, -6.85, -4.75, -2.65...