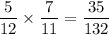Question

Steve has 12 biscuits in a tin.

There are 7 digestive and 5 chocolate biscuits.
Steve takes two biscuits at random from the tin.
Work out the probability that he chooses two different types of biscuits.

Answer 1

35/132 = 0.27 (nearest hundredth)

Step-by-step explanation:

Total number of biscuits = 12

Number of digestives = 7

Number of chocolate biscuits = 5

The probability of the first biscuit being a digestive is 7/12

As the first biscuit was not replaced, the total number of biscuits is now 11.

So the probability of the second biscuit being chocolate is 5/11

Therefore, the probability of the first biscuit being a digestive AND the second being chocolate is:

`(7)/(12)*(5)/(11)=(35)/(132)`

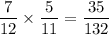
Similarly,

The probability of the first biscuit being chocolate is 5/12

As the first biscuit was not replaced, the total number of biscuits is now 11.

So the probability of the second biscuit being a digestive is 7/11

Therefore, the probability of the first biscuit being chocolate AND the second being a digestive is:

`(5)/(12)*(7)/(11)=(35)/(132)`

Answer 2

0.53 is the probability that he chooses two different types of biscuits.

Step-by-step explanation:

• digestive biscuits: 7

• chocolate biscuits: 5

• total biscuits: 12

probability:

`\rightarrow \sf (7)/(12) *(5)/(11) + (5)/(12) * (7)/(11)`

`\rightarrow \sf (35)/(66)`

`\rightarrow \sf 0.53`