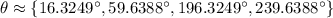Question

Kindly help answering the question.​

Answer 1

`\displaytstyle \theta \approx \left\{16.3249^\circ, 59.6388^\circ, 196.3249^\circ, 239.6388^\circ\right\}`

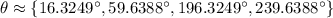
Or, their exact solutions:

`\displaystyle \theta = \left\{\arctan(2-√(2))/(2) , \arctan(2+√(2))/(2), 180^\circ + \arctan(2-√(2))/(2), 180^\circ + \arctan(2+√(2))/(2)\right\}`

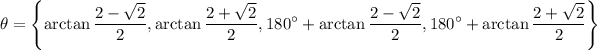
Explanation:

We want to solve the equation:

`\displaystyle 2\sec^2 \theta = 4\tan \theta + 1`

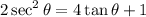
For 0° ≤ θ ≤ 360°.

Recall that tan²(θ) + 1 = sec²(θ). Substitute:

`\displaystyle 2\left(\tan^2 \theta + 1\right) = 4\tan \theta + 1`

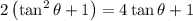
Distribute:

`\displaystyle 2\tan^2\theta + 2 = 4\tan\theta + 1`

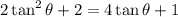
Isolate:

`\displaystyle 2\tan^2\theta - 4\tan\theta + 1 = 0`

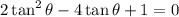
This is in quadratic form. Thus, we can solve it like a quadratic. Let u = tan(θ). Hence:

`\displaystyle 2u^2 - 4u + 1=0`

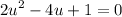
The equation is not factorable. Therefore, we can consider using the quadratic formula:

`\displaystyle x = (-b\pm√(b^2 -4ac))/(2a)`

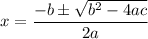
In this case, a = 2, b = -4, and c = 1. Substitute and evaluate:

`\displaytstyle \begin{aligned} u &= (-(-4)\pm√((-4)^2 - 4(2)(1)))/(2(2)) \\ \\ &= (4\pm√(8))/(4) \\ \\ &= (4\pm2√(2))/(4) \\ \\ &= (2\pm√(2))/(2)\end{aligned}`

Therefore:

`\displaystyle u = (2+√(2))/(2) \approx 1.7071\text{ or } u = (2-√(2))/(2)\approx 0.2929`

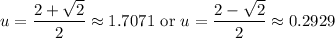
Back-substitute:

`\displaystyle \tan\theta = (2+√(2))/(2) \text{ or } \tan \theta = (2-√(2))/(2)`

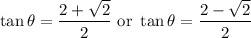
Take the inverse tangent of both equations. Hence:

`\displaystyle \theta = \arctan(2+√(2))/(2) \approx 59.6388^\circ\text{ or } \theta = \arctan(2-√(2))/(2)\approx 16.3249^\circ`

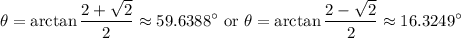
The same value of tangent occurs twice in every full rotation. Hence, by reference angles, the other two solutions are:

`\displaystyle \theta = 180^\circ + \arctan(2+√(2))/(2) \approx 239.6388^\circ \\ \\ \theta = 180^\circ + \arctan(2-√(2))/(2) \approx 196.3249^\circ`

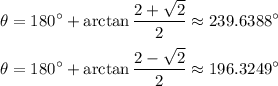
In conclusion, the four solutions are:

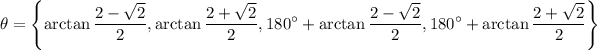`\displaystyle \theta = \left\{\arctan(2-√(2))/(2) , \arctan(2+√(2))/(2), 180^\circ + \arctan(2-√(2))/(2), 180^\circ + \arctan(2+√(2))/(2)\right\}`Or, approximately:

`\displaytstyle \theta \approx \left\{16.3249^\circ, 59.6388^\circ, 196.3249^\circ, 239.6388^\circ\right\}`