Answer:
a = - 2, remainder = 21
Explanation:
The Remainder theorem states that if f(x) is divided by (x - a) the remainder is f(a)
Since f(x) is divisible by (x - a) then remainder is zero , then
f(a) = 2a³ - 7a² + 7a² + 16 = 0 , that is
2a³ + 16 = 0 ( subtract 16 from both sides )
2a³ = - 16 ( divide both sides by 2 )
a³ = - 8 ( take the cube root of both sides )
a =
![\sqrt[3]{-8}](https://img.qammunity.org/2022/formulas/mathematics/high-school/c1fzdmssv9y4dla4nzzbvw3o3luhknjiiq.png) = - 2
= - 2
Then
f(x) = 2x³ - 7x² - 14x + 16
Evaluate f(-
 ) for remainder on division by (2x + 1)
) for remainder on division by (2x + 1)
f(-
 ) = 2(-
) = 2(-
 )³ - 7(-
)³ - 7(-
 )² - 14(-
)² - 14(-
 ) + 16
) + 16
= 2(-
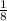 ) - 7(
) - 7(
 ) + 7 + 16
) + 7 + 16
= -
 -
-
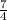 + 23
+ 23
= -
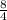 + 23
+ 23
= - 2 + 23
= 21