Answer:
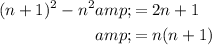
Where ? = 2.
Explanation:
We want to prove that the difference of the squares of two successive integers is equal to the sum of the integers.
In other words, we want to show that for any given integer n:
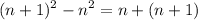
From the original equation, expand:
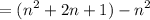
Combine like terms:
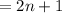
And rewrite. Hence:
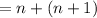
Therefore:
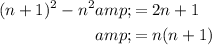
In conclusion, ? = 2.