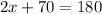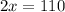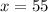Answer:
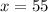 °
°
Explanation:
An isosceles triangle is a triangle with two congruent sides. One can see that the given triangle is an isosceles triangle, as two sides have a side length of (5) units. One property of an isosceles triangle is the base angles theorem. This theorem states that the angles opposite the congruent sides of an isosceles triangle are congruent. In this situation, this means that two angles have a measure of (x) degrees. As a given, the sum of angles in any triangle is (180) degrees. Thus, one can form an equation, and solve for the unknown, (x):
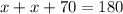
Simplify,
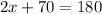
Inverse operations,