Answer:
F = 7.68 10¹¹ N, θ = 45º
Step-by-step explanation:
In this exercise we ask for the net electric force. Let's start by writing the configuration of the charges, the charges of the same sign must be on the diagonal of the cube so that the net force is directed towards the interior of the cube, see in the attached numbering and sign of the charges
The net force is
F_ {net} = F₂₁ + F₂₃ + F₂₄
bold letters indicate vectors. The easiest method to solve this exercise is by using the components of each force.
let's use trigonometry
cos 45 = F₂₄ₓ / F₂₄
sin 45 = F_{24y) / F₂₄
F₂₄ₓ = F₂₄ cos 45
F_{24y} = F₂₄ sin 45
let's do the sum on each axis
X axis
Fₓ = -F₂₁ + F₂₄ₓ
Fₓ = -F₂₁₁ + F₂₄ cos 45
Y axis
F_y = - F₂₃ + F_{24y}
F_y = -F₂₃ + F₂₄ sin 45
They indicate that the magnitude of all charges is the same, therefore
F₂₁ = F₂₃
Let's use Coulomb's law
F₂₁ = k q₁ q₂ / r₁₂²
the distance between the two charges is
r = a
F₂₁ = k q² / a²
we calculate F₂₄
F₂₄ = k q₂ q₄ / r₂₄²
the distance is
r² = a² + a²
r² = 2 a²
we substitute
F₂₄ = k q² / 2 a²
we substitute in the components of the forces
Fx =
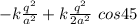
Fx =
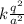 ( -1 + ½ cos 45)
( -1 + ½ cos 45)
F_y = k \frac{q^2}{a^2} ( -1 + ½ sin 45)
We calculate
F₀ = 9 10⁹ 4.25² / 0.440²
F₀ = 8.40 10¹¹ N
Fₓ = 8.40 10¹¹ (½ 0.707 - 1)
Fₓ = -5.43 10¹¹ N
remember cos 45 = sin 45
F_y = - 5.43 10¹¹ N
We can give the resultant force in two ways
a) F = Fₓ î + F_y ^j
F = -5.43 10¹¹ (i + j) N
b) In the form of module and angle.
For the module we use the Pythagorean theorem
F =

F = 5.43 10¹¹ √2
F = 7.68 10¹¹ N
in angle is
θ = 45º