Hello again! This is another Calculus question to be explained. The prompt reads that "If f(x) is a twice-differentiable function such that f(2) = 2 and (dy)/(dx) = 6√(x^2 …

Question

Hello again! This is another Calculus question to be explained.

The prompt reads that "If f(x) is a twice-differentiable function such that f(2) = 2 and
`(dy)/(dx)` =
`6√(x^2 + 3y^2)`, then what is the value of
`(d^2y)/(dx^2)` at x = 2?"

My initial calculation lead to 12, but then I guessed 219 as the answer and it was correct. Would any kind soul please explain why the answer would be 219? Thank you so much!

Answer 1

See explanation.

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

Functions

• Function Notation

• Exponential Property [Rewrite]:
  `\displaystyle b^(-m) = (1)/(b^m)`
• Exponential Property [Root Rewrite]:
  `\displaystyle \sqrt[n]{x} = x^{(1)/(n)}`

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Derivative Property [Addition/Subtraction]:
`\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Explanation:

We are given the following and are trying to find the second derivative at x = 2:

`\displaystyle f(2) = 2`

`\displaystyle (dy)/(dx) = 6√(x^2 + 3y^2)`

We can differentiate the 1st derivative to obtain the 2nd derivative. Let's start by rewriting the 1st derivative:

`\displaystyle (dy)/(dx) = 6(x^2 + 3y^2)^\big{(1)/(2)}`

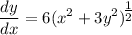
When we differentiate this, we must follow the Chain Rule:
`\displaystyle (d^2y)/(dx^2) = (d)/(dx) \Big[ 6(x^2 + 3y^2)^\big{(1)/(2)} \Big] \cdot (d)/(dx) \Big[ (x^2 + 3y^2) \Big]`

Use the Basic Power Rule:

`\displaystyle (d^2y)/(dx^2) = 3(x^2 + 3y^2)^\big{(-1)/(2)} (2x + 6yy')`

We know that y' is the notation for the 1st derivative. Substitute in the 1st derivative equation:

`\displaystyle (d^2y)/(dx^2) = 3(x^2 + 3y^2)^\big{(-1)/(2)} \big[ 2x + 6y(6√(x^2 + 3y^2)) \big]`

Simplifying it, we have:

`\displaystyle (d^2y)/(dx^2) = 3(x^2 + 3y^2)^\big{(-1)/(2)} \big[ 2x + 36y√(x^2 + 3y^2) \big]`

We can rewrite the 2nd derivative using exponential rules:

`\displaystyle (d^2y)/(dx^2) = (3\big[ 2x + 36y√(x^2 + 3y^2) \big])/(√(x^2 + 3y^2))`

To evaluate the 2nd derivative at x = 2, simply substitute in x = 2 and the value f(2) = 2 into it:

`\displaystyle (d^2y)/(dx^2) \bigg| \limits_(x = 2) = (3\big[ 2(2) + 36(2)√(2^2 + 3(2)^2) \big])/(√(2^2 + 3(2)^2))`

When we evaluate this using order of operations, we should obtain our answer:

`\displaystyle (d^2y)/(dx^2) \bigg| \limits_(x = 2) = 219`

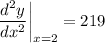
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Differentiation