Proof that : {sin}^(2) \theta + {cos}^(2) \:\theta= 1 Thx. ​

Question

Proof that :

`{sin}^(2) \theta + {cos}^(2) \:\theta= 1`
Thx.
​

Answer 1

Solution given:

Right angled triangle ABC is drawn where <C=
`\theta`

we know that

`\displaystyle Sin\theta=(opposite)/(hypotenuse) =(AB)/(AC)`

`\displaystyle Cos\theta=(adjacent)/(hypotenuse)=(BC)/(AC)`

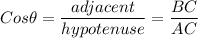
Now

left hand side

`\displaystyle {sin}^(2) \theta + {cos}^(2) \:\theta`

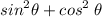
Substituting value

`((AB)/(AC))²+((BC)/(AC))²`

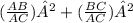
distributing power

`(AB²)/(AC²)+(BC²)/(AC²)`

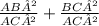
Taking L.C.M

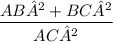`\displaystyle (AB²+BC²)/(AC²)`....[I]

In ∆ABC By using Pythagoras law we get

`\boxed{\green{\bold{Opposite²+adjacent²=hypotenuse²}}}`

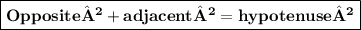
AB²+BC²=AC²

Substituting value of AB²+BC² in equation [I]

we get

`\displaystyle (AC²)/(AC²)`

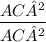
=1

Right hand side

proved