Question

Helppp!!!!!

Please!!!

{ is question #1 is right?? }
{ i need help with question #2 please }

Please!!
Helppp!!!!!

Answer 1

fyi b's answer has imaginary numbers in it...

Imaginary: 1 +
`(√(2i) )/(2 )`

Imaginary: 1 -
`(√(2i) )/(2 )`

Explanation:

`2x^(2) - 4x -3 = 0`

`\sqrt{-4^(2) -4(2)(3)}` =
`√(-8)` ... the negative root will produce imaginary solutions

Answer 2

9514 1404 393

Answer:

1a. -4, 3/4

1b. 1-0.71i, 1+0.71i

Explanation:

The directions tell you to use the quadratic formula. Factoring may get you the solution somewhat more easily, but does not comply with the directions.

The quadratic formula tells you ...

`\text{The solution to }ax^2+bx+c=0\text{ is given by }\\\\x=(-b\pm√(b^2-4ac))/(2a)`

__

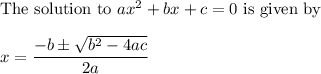
1a. a=4, b=13, c=-12

`x=(-13\pm√(13^2-4(4)(-12)))/(2(4))=(-13\pm√(361))/(8)=(-13\pm19)/(8)\\\\x=\left\{-4,(3)/(4)\right\}`

__

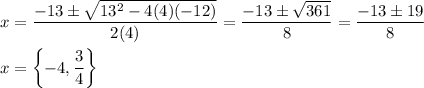
1b. After adding 3 to both sides, a=2, b=-4, c=3

`x=(-(-4)\pm√((-4)^2-4(2)(3)))/(2(2))=(4\pm√(-8))/(4)=1\pm(√(2))/(2)i\\\\x=\left\{1-(√(2))/(2)i,1+(√(2))/(2)i\right\}\approx\{1-0.71i,1+0.71i\}`