Question

How many terms are in the following geometric sequence? Type your numerical answer only. Do not type any additional characters.

0.0625, 0,25, 1, 4194304

Answer 1

Given:

The given geometric sequence is:

0.0625, 0.25, 1, ..., 4194304

To find:

The number of terms in the given geometric sequence.

Solution:

We have,

0.0625, 0.25, 1, ..., 4194304

Here, the first term is 0.0625 and the common ratio is:

`r=(0.25)/(0.0625)`

`r=4`

The nth term of a geometric sequence is:

`a_n=ar^(n-1)`

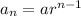
Where, a is the first term and r is the common ratio.

Putting
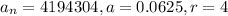`a_n=4194304, a=0.0625, r=4` in the above formula, we get

`4194304=0.0625(4)^(n-1)`

`(4194304)/(0.0625)=(4)^(n-1)`

`67108864=(4)^(n-1)`

`4^(13)=(4)^(n-1)`

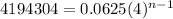
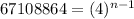
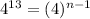
On comparing both sides, we get

`13=n-1`

`13+1=n`

`14=n`

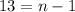
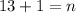
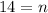
Therefore, the number of terms in the given geometric sequence is 14.