Question

8. A boat moving initially at 6.5 km hr due southwest crosses a river that is flowing due south at 3 km hr.

What is the magnitude and direction of the boat relative to the ground? If the river is 1.5 mi wide how long
does it take the boat to cross?

Answer 1

a) v = 8,878 km / h, θ’= 238.8º, b) t = 1890.9 s

Step-by-step explanation:

a) In this exercise we must find the resulting speed of the boat.

Let's use trigonometry to break down the speed of the boat (v1)

cos 225 = v₁ₓ / v₁

sin 225 = v_{1y} / v₁

v₁ₓ = v₁ soc 225

v_{1y} = v₁ sin 225

v₁ₓ = 6.5 cos 225 = -4.596 km / h

v_{1y} = 6.5 sin 225 = -4.596 km / h

to find the velocity we add each component

vₓ = v₁ₓ

vₓ = - 4,596 km / h

v_y = v_{1y} + v₂

v_y = -4.596 - 3

v_y = - 7,596 km / h

Now let's compose the speed

Let's use the Pythagorean theorem for the module

v =
`√(v_x^2 + v_y^2 )`

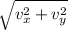
v = Ra 4.596² + 7.596²

v = 8,878 km / h

Let's use trigonometry for the direction

tan θ = v_y / vₓ

θ = tan⁻¹ v_y / vₓ

θ = tan⁻¹ (
`(-7.596)/( -4.596)` )

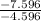θ = 58.8º

measured from the positive side of the x-axis

θ'= 180 + 58.8

θ’= 238.8º

b) Let's reduce the river width to the SI system

x = 1.5 miles (1,609 km / 1 mile) = 2,414 km

to cross the river the speed is on the x axis which is the width of the river

v = x / t

t = x / v

t = 2.414 /4.596

t = 0.525 h

let's reduce to the SI system

t = 0.525 h (3600 s / 1h)

t = 1890.9 s