Question

Find the slope of any line perpendicular to
the line through M(-1,5) and N(0.-3).

Answer 1

1/8

Explanation:

We want to find the slope of any line that is perpendicular to the line passing through the points M(-1, 5) and N(0, -3).

Recall that the slopes of perpendicular lines are negative reciprocals of each other. In other words, the slope of any line perpendicular to line MN must be the negative reciprocal of the slope of line MN.

Find the slope of MN using the slope formula:

`\displaystyle m_(MN) = (\Delta y)/(\Delta x) = ((-3)-(5))/((0)-(-1)) = (-8)/(1)=-8`

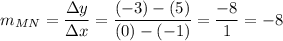
So, the slope of line MN is -8.

The slope of any line perpendicular to MN must be its negative reciprocal. The negative reciprocal of -8 is 1/8.

Therefore, the slope of any line perpendicular to the line passing through the points M(-1, 5) and N(0, -3) is 1/8.