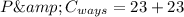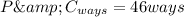Question

A certain baseball team has 23 players. Only nine can be on the field at a time. Each of the nine players on the field has a distinct field position: pitcher, catcher, first baseman, second baseman, third baseman, short stop, left field, right field, or center field. Assume for the moment that every player is qualified to play every position.

Required:
How many ways are there to fill either the pitcher or catcher field position (but not both) from among the 23 players (leaving the other field positions empty)?

Answer 1

`P \& C _(ways)=46ways`

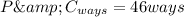
Explanation:

From the question we are told that:

Sample size
`n=23`

Generally the pitcher or catcher field position can be filled in

23 way respectively

Where

No. ways for to fill Pitcher

`P_(ways)=23 ways`

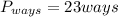
No. ways for to fill Catcher

`C_(ways)=23 ways`

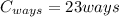
Therefore

Applying counting Principles

No. ways to fill both

`P \& C _(ways)=23+23`

`P \& C _(ways)=46ways`