Question

A waste management company is designing a rectangular construction dumpster that will be twice as long as it is wide and must hold 10 yd3 of debris. Find the dimensions of the dumpster that will minimize its surface area.

Answer 1

The dimensions are:

l = 2*1.96 = 3.92 yd

h = 5/(1.96)² = 1.30 yd

w = 1.96 yd

Explanation:

The volume is given by:

`V=l*w*h`

Where:

• l is the long
• w the wide
• h the height

We know that l = 2w, so we have:

`V=2w^(2)*h`

`10=2w^(2)*h`

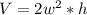
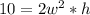
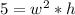`5=w^(2)*h` (2)

Now, the surface of this parallelepiped is:

`S=2wh+2lh+lw`

Using l = 2w:

`S=2wh+4wh+2w^(2)`

Using (2) we obtain the surface equation in terms of w.

`S=2w(5)/(w^(2))+4w(5)/(w^(2))+2w^(2)`

`S=2(5)/(w)+4(5)/(w)+2w^(2)`

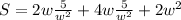
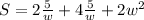
We need to take the derivative with respect to w to minimize the surface area.

`S=2(5)/(w)+4(5)/(w)+2w^(2)`

`S=(30)/(w)+2w^(2)`

`(dS)/(dw)=-(30)/(w^(2))+4w`

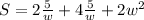
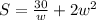
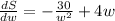
Now, let's equal it to zero.

`0=-(30)/(w^(2))+4w`

`(30)/(w^(2))=4w`

`w^(3)=(30)/(4)`

`w=1.96\: yd`

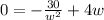
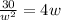
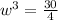
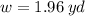
So, l = 2*1.96 = 3.92 yd and h = 5/(1.96)² = 1.30 yd

Therefore, the dimensions are:

l = 2*1.96 = 3.92 yd

h = 5/(1.96)² = 1.30 yd

w = 1.96 yd

I hope it helps you!