Question

If f is continuous for all x, which of the following integrals necessarily have the same value?

Answer 1

B

Explanation:

Given the three integrals, we want to determine which integrals necessarily have the same value.

We can let the first integral be itself.

For the second integral, we can perform a u-substitution. Let u = x + a. Then:

`\displaystyle du = dx`

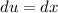
Changing our limits of integration:

`u_1=(0)+a=a \text{ and } u_2 = (b+a)+a = b+2a`

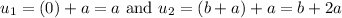
Thus, the second integral becomes:

`\displaystyle \int_(0)^(b+a)f(x+a)\, dx = \int_a^(b+2a) f(u)\, du`

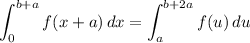
For the third integral, we can also perform a u-substitution. Let u = x + c. Then:

`\displaystyle du = dx`

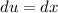
And changing our limits of integration:

`\displaystyle u_1=(a-c)+c=a \text{ and } u_2=(b-c)+c=b`

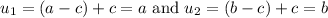
Thus, our third integral becomes:

`\displaystyle \int_(a-c)^(b-c)f(x+c)\, dx = \int_(a)^(b) f(u)\, du`

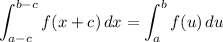
Since the only difference between f(x) and f(u) is the variable and both the first and third integral have the same limits of integration, our answer is B.