Question

Would you favor spending more federal tax money on the arts? Of a random sample of n1 = 222 women, r1 = 51 responded yes. Another random sample of n2 = 174 men showed that r2 = 49 responded yes. Does this information indicate a difference (either way) between the population proportion of women and the population proportion of men who favor spending more federal tax dollars on the arts? Use ???? = 0.05.

Answer 1

The p-value of the test is 0.242 > 0.05, which means that this information does not indicate a difference between the population proportion of women and the population proportion of men who favor spending more federal tax dollars on the arts.

Explanation:

Before solving this question, we need to understand the central limit theorem and subtraction of normal variables.

Central Limit Theorem

The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

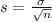For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
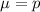`\mu = p` and standard deviation
`s = \sqrt{(p(1-p))/(n)}`

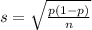
Subtraction between normal variables:

When two normal variables are subtracted, the mean is the difference of the means, while the standard deviation is the square root of the sum of the variances.

Women:

51 out of 222, so:

`p_1 = (51)/(222) = 0.2297`

`s_1 = \sqrt{(0.2297*0.7703)/(222)} = 0.0282`

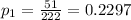
Men:

49 out of 174, so:

`p_2 = (49)/(174) = 0.2816`

`s_2 = \sqrt{(0.2816*0.7184)/(174)} = 0.0341`

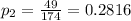
Does this information indicate a difference (either way) between the population proportion of women and the population proportion of men who favor spending more federal tax dollars on the arts?

Either way, so a two tailed test to see if the difference of proportions is different of 0.

At the null hypothesis, we test if it is not different of 0, so:

`H_0: p_1 - p_2 = 0`

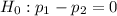
At the alternative hypothesis, we test if it is different of 0, so:

`H_1: p_1 - p_2 \\eq 0`

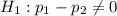
The test statistic is:

`z = (X - \mu)/(s)`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis, and s is the standard error.

0 is tested at the null hypothesis:

This means that
`\mu = 0`

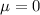
From the samples:

`X = p_1 - p_2 = 0.2297 - 0.2816 = -0.0519`

`s = √(s_1^2+s_2^2) = √(0.0282^2+0.0341^2) = 0.0442`

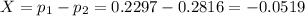
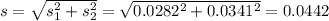
Value of the test statistic:

`z = (X - \mu)/(s)`

`z = (-0.0519 - 0)/(0.0442)`

`z = -1.17`

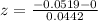
P-value of the test and decision:

The p-value of the test is the probability of the differences being of at least 0.0519, either way, which is P(|z| > 1.17), that is, 2 multiplied by the p-value of z = -1.17.

Looking at the z-table, z = -1.17 has a p-value of 0.121.

0.121*2 = 0.242

The p-value of the test is 0.242 > 0.05, which means that this information does not indicate a difference between the population proportion of women and the population proportion of men who favor spending more federal tax dollars on the arts.