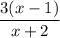Question

Your classmate simplified the following rational expression and asked you if you got the same answer. Determine whether the answer below is correct. If it is not correct, simplify the expression. Show all of your work.

Rational expression: (x^(2)-1) / (x^(2)-4x-5) ÷ (2x^(2)+4x) / (6x^(2)-30x)


Your friend's answer: (2x(x-1)(x+2)) / (6x(x-5)(x-5))

Answer 1

The friend's answer is incorrect.

The correct answer is:

`(3(x - 1))/(x + 2)`

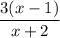
Explanation:

`(x^2 - 1)/(x^2 - 4x - 5) / (2x^2 + 4x)/(6x^2 - 30x) =`

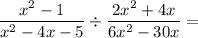
To divide by a fraction, multiply by its reciprocal.

`= (x^2 - 1)/(x^2 - 4x - 5) * (6x^2 - 30x)/(2x^2 + 4x)`

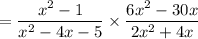
Multiply the numerators together. Multiply the denominators together.

`= ((x^2 - 1)(6x^2 - 30x))/((x^2 - 4x - 5)(2x^2 + 4x))`

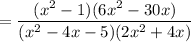
Factor every polynomial.

`= ((x - 1)(x + 1)(6x)(x - 5))/((x - 5)(x + 1)(2x)(x + 2))`

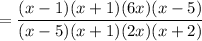
Divide the numerator and denominator by the common terms.

`= ((x - 1)(6))/((2)(x + 2))`

`= (3(x - 1))/(x + 2)`

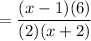
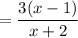
The friend's answer is incorrect.

The correct answer is:

`(3(x - 1))/(x + 2)`