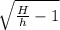Answer:
x = 2h
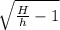
Step-by-step explanation:
This is an exercise in fluid mechanics, let's find the speed of the water in the hole
P₁ + ½ ρ v₁² + ρ g y₁ = P₂ + ½ ρ v₂² + ρ g y₂
where the subscript 1 is for the tank surface and the subscript 2 is for the depth of the hole
the pressure inside and outside the tank is the same
P₁ = P₂
we must measure the distance from the same reference point, let's locate it on the surface of the water
y₁ = 0
y₂ = h
Suppose the gap is small compared to the diameter of the tank
v₁ «v₂
v₂² = 2 g (0-h)
This is the speed of the outlet water in the tank, as the force is horizontal this speed is horizontal.
Let's use the projectile launch ratios
vₓ =
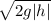
y = y₀ + v₀ t - ½ g t²
the height when reaching the floor is y = 0,
the initial height is measured from the floor therefore y₀ = H-h
0 = (H-h) + 0 - ½ g t²
t =
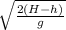
we look for the distance x traveled
x = vₓ t
x =
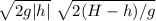
x =
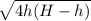
x = 2h