Question

The length of a rectangle is 13 centimeters less than three times its width. Its area is 56 square centimeters. Find the dimensions of the rectangle. Use the​ formula, area=length*width.

Answer 1

The dimensions of the rectangle are 8 by 7 centimeters.

Explanation:

The length of a rectangle is 13 centimeters less than three times its width. In other words:

`\ell = 3w-13`

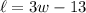
Given that the area of the rectangle is 56 square centimeters, we want to determine its dimensions.

Recall that the area of a rectangle is given by:

`A = w \ell`

Substitute in known values and equations:

`(56)=w(3w-13)`

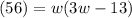
Solve for w. Distribute:

`3w^2-13w=56`

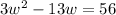
Isolate the equation:

`3w^2-13w-56=0`

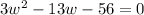
Factor. We want to find two numbers that multiply to 3(-56) = -168 and that add to -13.

-21 and 8 suffice. Hence:

`3w^2 - 21w + 8w - 56 = 0 \\ \\ 3w(w-7) + 8(w-7) = 0 \\ \\ (3w+8)(w-7) = 0`

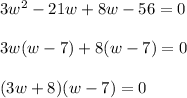
Zero Product Property:

`3w+8=0\text{ or } w-7=0`

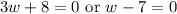
Solve for each case:

`\displaystyle w = -(8)/(3) \text{ or } w=7`

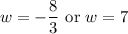
Since the width cannot be negative, we can ignore the first solution.

Therefore, the width of the rectangle is seven centimeters.

Thus, the length will be:

`\ell = 3(7) - 13 = 8`

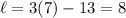
Thus, the dimensions of the rectangle are 8 by 7 centimeters.