Question

Using a secant and a tangent, find angle WVT.

Answer 1

`m\angle WVT=40^(\circ)`

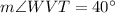
Explanation:

When two secants or a secant and a tangent of a circle intersect outside the circle, the measure of the acute angle formed is equal to half of the positive difference of smaller and larger arc formed.

Therefore, we have the equation:

`m\angle WVT=(1)/(2)(\widehat{TW}-\widehat{UW}),\\3x+4=(1)/(2)(14x+7-(7x+11))`

Distribute:

`3x+4=(1)/(2)(14x+7-7x-11),\\\\3x+4=(1)/(2)(7x-4),\\\\3x+4=3.5x-2`

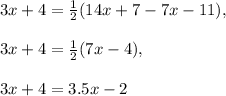
Add 2 to both sides and subtract
`3x` from both sides:

`6=0.5x`

Divide both sides by 1/2:

`x=(6)/((1)/(2))=6\cdot 2=12`

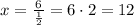
Now substitute
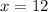`x=12` into
`3x+4`:

`m\angle WVT=3(12)+4,\\m\angle WVT=36+4,\\m\angle WVT=\boxed{40^(\circ)}`