Answer:
See Below.
Explanation:
We want to show that the function:
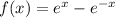
Increases for all values of x.
A function is increasing whenever its derivative is positive.
So, find the derivative of our function:
![\displaystyle f'(x) = (d)/(dx)\left[e^x - e^(-x)\right]](https://img.qammunity.org/2022/formulas/mathematics/college/rit8er30jmkl0z1njjoy4bk32u5xivh2vl.png)
Differentiate:
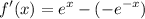
Simplify:

Since eˣ is always greater than zero and e⁻ˣ is also always greater than zero, f'(x) is always positive. Hence, the original function increases for all values of x.