Question

The life of light bulbs is distributed normally. The standard deviation of the lifetime is 20 hours and the mean lifetime of a bulb is 500 hours. Find the probability of a bulb lasting for between 480 and 526 hours.

Answer 1

The probability of a bulb lasting for between 480 and 526 hours=0.74454

Explanation:

We are given that

Standard deviation of the lifetime,
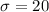`\sigma=20`hours

Mean,
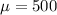`\mu=500`hours

We have to find the probability of a bulb lasting for between 480 and 526 hours.

`P(480<x<526)=P((480-500)/(20)<(x-\mu)/(\sigma)<(526-500)/(20))`

`P(480<x<526)=P(-1<Z<1.3)`

`P(480<x<526)=P(Z<1.3)-P(Z<-1)`

`P(480<x<526)=0.90320-0.15866`

`P(480<x<526)=0.74454`

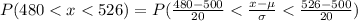
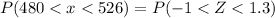
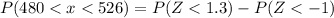
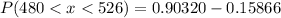
Hence, the probability of a bulb lasting for between 480 and 526 hours=0.74454