Answer:
See Below.
Explanation:
We want to prove that:
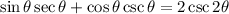
Let secθ = 1 / cosθ and cscθ = 1 / sinθ:

Creat a common denominator. Multiply the first fraction by sinθ and the second by cosθ. Hence:
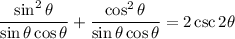
Combine fractions:
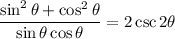
Simplify. Recall that sin²θ + cos²θ = 1:
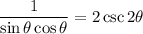
Multiply the fraction by two:
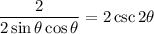
Recall that sin2θ = 2sinθcosθ. Hence:
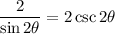
By definition:
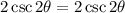
Hence proven.