Answer:

Step-by-step explanation:
Given :
The first dark fringe is for m = 0
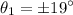
Now we know for a double slit experiments , the position of the dark fringes is give by :
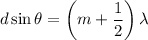
The ratio of distance between the two slits, d to the light's wavelength that illuminates the slits, λ :
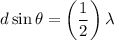 (since, m = 0)
(since, m = 0)
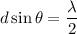
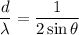
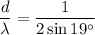

Therefore, the ratio is
 or 1 : 1.54
or 1 : 1.54