Question

g A. (Points: 7) Compute (without using a calculator) 241^257 mod 12 B. (Points: 3) Compute Z*20 C. (Points: 6) Find the multiplicative inverse of 7 in Z19

Answer 1

`241^(257)\ mod\ 12 =1`

`7 * 20 = 140`

`(1)/(700)`

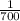
Explanation:

Solving (a): 241^257 mod 12

To do this, we simply calculate
`241\ mod\ 12`

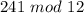
Because
`a\ mod\ b = a^n\ mod\ b`

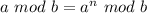
The highest number less than or equal to 241 that is divisible by 12 is 240; So:

`241\ mod\ 12 = 241- 240`

`241\ mod\ 12 =1`

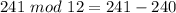
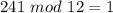
Hence:

`241^(257)\ mod\ 12 =1`

Solving (b): 7 * 20

`7 * 20 = 140`

Solving (c): Multiplicative inverse of 7 in 719

The position of 7 in 719 is 700

So, the required inverse is 1/700 ---- i.e. we simply divide 1 by the number