Mr. Pinter's class has twice as many students as Mrs. Rupert's class. Mrs. Althouse's class has 20 less than three times Mrs. Rupert's class. Together they h…

Question

asked May 13, 2022 166k views

1 Answer

Pavel Shishpor · Answer 1 · 2022-05-19T05:57:21+0000

Answer:

Mr. Pinter's class has 42 students, Mrs. Rupert's class has 21 students, and Mrs. Althouse's class has 43 students.

Explanation:

This question is solved using a system of equations.

I am going to say that:

Mr. Pinter's class has x students.

Mrs. Rupert's class has y students.

Mrs. Althouse's class has z students.

Mr. Pinter's class has twice as many students as Mrs. Rupert's class.

This means that:

x = 2y

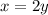
Mrs. Althouse's class has 20 less than three times Mrs. Rupert's class.

This means that:

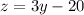
z = 3y - 20

Together they have 106 students.

This means that:

x + y + z = 106

We have x and z has a function of y, so:

2y + y + 3y - 20 = 106

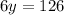
6y = 126

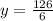
y = (126)/(6)

y = 21

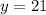
And:

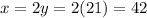
x = 2y = 2(21) = 42

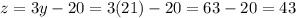
z = 3y - 20 = 3(21) - 20 = 63 - 20 = 43

Mr. Pinter's class has 42 students, Mrs. Rupert's class has 21 students, and Mrs. Althouse's class has 43 students.