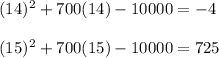Question

a manufacturer has determined that if his company sells x items per day then their profit is given by P=-x^2+ 700 x-10000 euros. . How many items must be sold each day in order to make a profit

Answer 1

15

Explanation:

To find the minimum amount of items, x, that need to be sold for the manufacturer to make a profit, we can use the quadratic formula

`x = \frac{-b+\sqrt{b^(2)-4ac } }{2a}; x= \frac{-b-\sqrt{b^(2)-4ac } }{2a}`

`x= \frac{-700+\sqrt{700^(2)-4(a)(-10000) } }{2(1)}; x= \frac{-700-\sqrt{700^(2)-4(a)(-10000) } }{2(1)}`

`x= (-700+√(530000) )/(2); x= (-700-√(530000) )/(2)`

`x=(-700+100√(53) )/(2); x=(-700-100√(53) )/(2);`

`x=-350 + 50\sqrt53 = 14.005; x = -350 - 50\sqrt53 = -714.005`

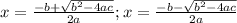
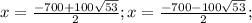
In context of the problem, we can only rely on the positive value, as the negative value would lead to a loss of profit.

`(-714.005)^2+700(-714.005)-10000=-0.360`

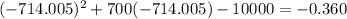
Furthermore, we must round to the nearest whole number, as you cannot make part of an item.

Lastly, if you were to plug in 14 into the equation for Profit, you would still have a negative number (i.e. a negative profit), thus requiring the manufacturer to make no less than 15 items to make a profit:

`(14)^2+700(14)-10000=-4\\\\(15)^2+700(15)-10000=725`