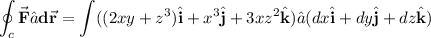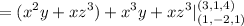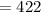Explanation:
Given:
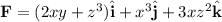
This field will have a scalar potential
 if it satisfies the condition
if it satisfies the condition
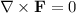 . While the first x- and y- components of
. While the first x- and y- components of
 are satisfied, the z-component doesn't.
are satisfied, the z-component doesn't.
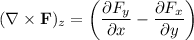
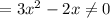
Therefore the field is nonconservative so it has no scalar potential. We can still calculate the work done by defining the position vector
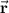 as
as
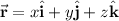
and its differential is

The work done then is given by