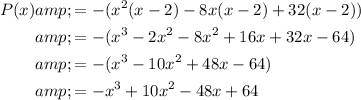Question

Find the polynomial of minimum degree, with real coefficients, zeros at x=4+4i and x=2, and y-intercept at 64

Answer 1

`\displaystyle -x^3+10x^2-48x+64`

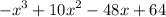
Explanation:

We want to find the minimum-degree polynomial with real coefficients and zeros at:

`x= 4+4i\text{ and } x = 2`

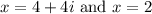
As well as a y-intercept of 64.

By the Complex Root Theorem, if a + bi is a root, then a - bi is also a root.

So, a third root will be 4 - 4i.

The factored form of a polynomial is given by:

`P(x)=a(x-p)(x-q)...`

Where a is the leading coefficient and p and q are the zeros. More factors can be added if necessary.

Substitute:

`P(x)=a(x-(2))(x-(4+4i))(x-(4-4i))`

Since we want the minimum degree, we won't need to add any exponents.

Expand the second and third factors:

`\displaystyle \begin{aligned} (x-(4+4i))(x-(4-4i))&=(x-4-4i)(x-4+4i) \\ &= x(x-4-4i)-4(x-4-4i)+4i(x-4-4i)\\ &=x^2-4x-4ix-4x+16+16i+4ix-16i-16i^2\\ &= x^2-8x+32\end{aligned}`

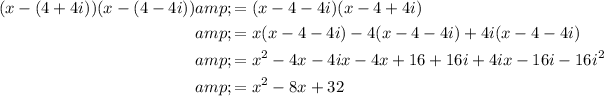
Hence:

`P(x)=a(x-2)(x^2-8x+32)`

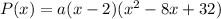
Lastly, we need to determine a. Since the y-intercept is y = 64, this means that when x = 0, y = 64. Thus:

`64=a(0-2)(0^2-8(0)+32)`

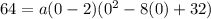
Solve for a:

`-64a=64\Rightarrow a=-1`

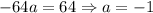
Our factored polynomial is:

`P(x)=-(x-2)(x^2-8x+32)`

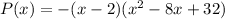
Finally, expand:

`\displaystyle \begin{aligned} P(x) &=-(x^2(x-2)-8x(x-2)+32(x-2)) \\&=-(x^3-2x^2-8x^2+16x+32x-64)\\&=-(x^3-10x^2+48x-64)\\&= -x^3+10x^2-48x+64\end{aligned}`