Answer:
The value of the limit is 0.
Explanation:
We are given the following limit:
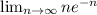
Simplifying the function:
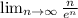
Replacing infinity at the numerator and denominator, we get infinity divided by infinity. Thus, L'Hospital Theorem can be applied, which means that we find the limit of the derivative of the numerator and the denominator.
Derivative of n is 1, of
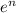 is
is
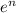
Then
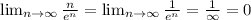
The value of the limit is 0.