Question

I have to use completing the square then put it in vertex form, and I have no clue how the hell do to that.

Answer 1

y=8(x+1)²-2

Explanation:

Completing the square is a method of factorising. x²+bx+c=0 becomes x²+bx+(
`(1)/(2)`b)²-(
`(1)/(2)`b)²+c=0. This then gets converted to make an equation of (x+
`(1)/(2)`b)²+(-(
`(1)/(2)`b)²+c)=0.

Vertex form is y=a(x-h)²+k.

8x²+16x+6=0 must first be divided by 8 to 8(x²+2x+
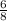`(6)/(8)`)=0 (as there cannot be a coefficient for x²).

This will become 8(x²+2x+
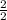`(2)/(2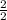)`²-
`(2)/(2)`²+
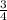`(3)/(4)`)=0.

From there, using the method above, we can convert it to 8[(x+1)²-1+
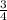`(3)/(4)`]=0.

Solving this gets 8[(x+1)²-
`(1)/(4)`]=0.

With 8 as a, 1 as -h, and 8×-
`(1)/(4)` (-2) as k, we can input this into vertex format to get the result of y=8(x+1)²-2.

**This equation involves completing the square and vertex form, which you may wish to revise. I'm always happy to help!