Question

In circle A below, chord BC and diameter DAE intersect at F. If arc CD = 46° and arc BE = 78°, what is m_BFE? D B А​

Answer 1

Given:

Consider the below figure attached with this question.

In circle A below, chord BC and diameter DAE intersect at F.

The arc CD = 46° and arc BE = 78°.

To find:

The measure of angle BFE.

Solution:

According to intersecting chords theorem, if two chords intersect inside the circle then the angle on the intersection is the average of intercepted arcs.

Using intersecting chords theorem, we get

`m\angle BFE=(1)/(2)(m(arcCD)+m(arcBE))`

`m\angle BFE=(1)/(2)(46^\circ+78^\circ)`

`m\angle BFE=(1)/(2)(124^\circ)`

`m\angle BFE=62^\circ`

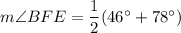
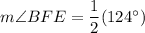
Therefore, the measure of angle BFE is 62°.