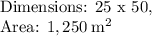Question

A rectangular area is to be enclosed using an existing

wall as one side 100m of fencing are available for the

three side. It is desire to make the areas as large as

possible. Find the necessary dimension of the

enclosure and the maximum area.​

Answer 1

`\text{Dimensions: 25 x 50},\\\text{Area: }1,250\:\mathrm{m^2}`

Explanation:

Let the one of the side lengths of the rectangle be
`x` and the other be
`y`.

We can write the following equations, where
`x` will be the side opposite to the wall:

`x+2y=100,\\xy=\text{Area}`

From the first equation, we can isolate
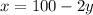`x=100-2y` and substitute into the second equation:

`(100-2y)y=\text{Area},\\-2y^2+100=\text{Area}`

Therefore, the parabola
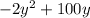`-2y^2+100y` denotes the area of this rectangular enclosure. The maximum area possible will occur at the vertex of this parabola.

The x-coordinate of the vertex of a parabola in standard form
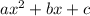`ax^2+bx+c` is given by
`(-b)/(2a)`.

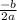Therefore, the vertex is:

`(-100)/(2(-2))=(100)/(4)=25`

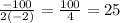
Plug in
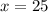`x=25` to the equation to get the y-coordinate:

`-2(25^2)+100(25)=\boxed{1,250}`

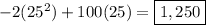
Thus the vertex of the parabola is at
`(25, 1250)`. This tells us the following:

• The maximum area occurs when one side (y) of the rectangle is equal to 25
• The maximum area of the enclosure is 1,250 square meters
• The other dimension, from
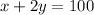  `x+2y=100`, must be
  `50`

And therefore, the desired answers are:

`\text{Dimensions: 25 x 50},\\\text{Area: }1,250\:\mathrm{m^2}`