Question

1. State the order and type of each transformation of the graph of the function f(x) = 6 0.2x as compared to the graph of the base function.​

Answer 1

madsfxe is equal i believe hope this helps

Answer 2

1. The order of transformation for the graph of the function
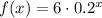`\( f(x) = 6 \cdot 0.2^x \)` compared to the base function
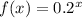`\( f(x) = 0.2^x \)` is a vertical stretch by a factor of 6.

Step-by-step explanation:

The given function is
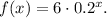`\( f(x) = 6 \cdot 0.2^x \).` To understand the transformation, let's compare it with the base function
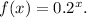`\( f(x) = 0.2^x \).` The general form for a vertical stretch or compression is
`\( g(x) = a \cdot f(x) \)`, where
`\( a \)` is the stretch or compression factor.

In this case,
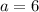`\( a = 6 \)`, which means there is a vertical stretch by a factor of 6. The calculation involves evaluating the function for specific values of
`\( x \)` and observing the corresponding
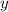`\( y \)` values. For example, if
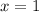`\( x = 1 \)`, in the base function,
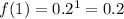`\( f(1) = 0.2^1 = 0.2 \)`, and in the transformed function,
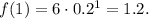`\( f(1) = 6 \cdot 0.2^1 = 1.2 \).` This multiplication by 6 represents the vertical stretch.

The order of transformation is determined by the sequence in which multiple transformations occur. In this case, there is a single transformation—vertical stretching. The type of transformation is identified as a vertical stretch because the
`\( y \)-values` are stretched by a factor of 6, making the graph taller compared to the base function. Therefore, the final answer is a vertical stretch by a factor of 6.