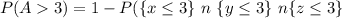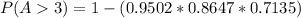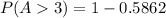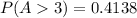Question

In a small metropolitan area, annual losses due to storm, fire, andtheft are assumed to be independent, exponentially distributed random variableswith respective means 1.0, 1.5, 2.4. Determine the probability that the maximumof these losses exceeds 3.

Answer 1

`0.4138`

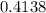
Explanation:

Given

`x \to storm`

`\mu_x = 1.0`

`y \to fire`

`\mu_y = 1.5`

`z \to theft`

`\mu_z = 2.4`

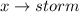
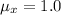
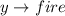
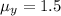
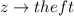
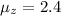
Let the event that the above three factors is greater than 3 be represented as:

`P(A > 3)`

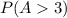
Using complement rule, we have:

`P(A > 3) = 1 - P(A \le 3)`

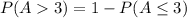
This gives:

`P(A > 3) = 1 - P(\{x \le 3\}\ n\ \{y \le 3\}\ n \{z \le 3\}\)`

-----------------------------------------------------------------------------------------------------------

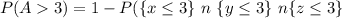
The exponential distribution formula of each is:

`P(x \le k) = 1 - e^{-(k)/(\mu)}`

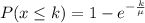
So, we have:

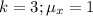
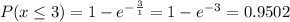
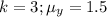
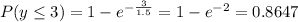
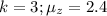
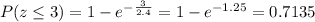
`k = 3; \mu_x = 1`

`P(x \le 3) = 1 - e^{-(3)/(1)} = 1 - e^(-3) = 0.9502`

`k=3; \mu_y = 1.5`

`P(y \le 3) = 1 - e^{-(3)/(1.5)} = 1 - e^(-2) = 0.8647`

`k = 3; \mu_z = 2.4`

`P(z \le 3) = 1 - e^{-(3)/(2.4)} = 1 - e^(-1.25) = 0.7135`

-----------------------------------------------------------------------------------------------------------

`P(A > 3) = 1 - P(\{x \le 3\}\ n\ \{y \le 3\}\ n \{z \le 3\}\)`

`P(A > 3) = 1 - (0.9502 * 0.8647 *0.7135)`

`P(A > 3) = 1 - 0.5862`

`P(A > 3) = 0.4138`