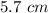Answer:
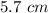
Explanation:
Given
Rectangle has an area of
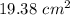
Suppose rectangle length and width are
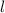 and
and
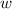
If each side is increased by
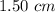
Area becomes
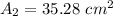
We can write
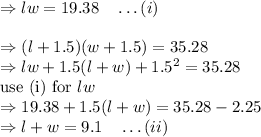
Substitute the value of width from (ii) in equation (i)
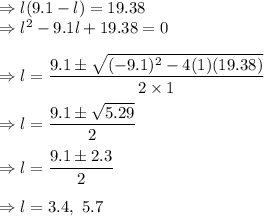
Width corresponding to these lengths
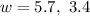
Therfore, we can write the length of the longer side is