Which equation in rectangular form describes the parametric equations x=2-3 cos t and y=1+4 sin t?

Question

asked Jun 13, 2022 183k views

1 Answer

Olivier Amblet · Answer 1 · 2022-06-18T14:20:13+0000

Answer:

The parametric equations represents an ellipse by the rectangular equation
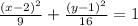((x-2)^(2))/(9) + ((y-1)^(2))/(16) = 1 .

Explanation:

We proceed to use the following trigonometric identity to derive an expression in rectangular form:

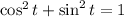$\cos^(2) t + \sin^(2) t = 1$ (1)

Where:

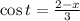$\cos t = (2-x)/(3)$ and
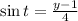
$\sin t = (y-1)/(4)$

Then, we expand the expression as follows:

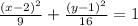((x-2)^(2))/(9) + ((y-1)^(2))/(16) = 1 (2)

The parametric equations represents an ellipse by the rectangular equation
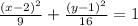((x-2)^(2))/(9) + ((y-1)^(2))/(16) = 1 .