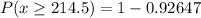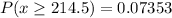Question

Suppose that 50% of the watches produced by a certain factory are defective. A store buys a box with 400 watches produced by this factory. Assume That this is a random sample.(a) Write an expression for the exact probability that at least 215 watches out ofthe 400 are defective. You do not need to numerically evaluate it.(b) Argue whether the normal or the Poisson approximation is appropriate to es-timate the above probability and then estimate it.

Answer 1

`(a)\ P(x \ge 215)`

`(b)\ P(x \ge 214.5) = 0.07353`

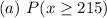
Explanation:

Given

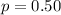`p = 0.50` ---- proportion of watches with defects

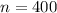`n = 400` --- Number of watches

Solving (a): Represent at least 215 of 400 are defective

In inequalities, at least means:
`\ge`

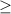
So, the probability is represented as:
`P(x \ge 215)`

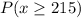
Solving (b): Calculate
`P(x \ge 215)`

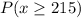
Normal or Poisson: Normal distribution is characterized by 2 parameters
`\mu` and
`\sigma`.

These two parameters can be easily calculated from the given parameters in the question. So, we solve using normal distribution

Start by calculating the mean

`\mu =np`

`\mu = 0.50 * 400`

`\mu = 200`

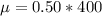
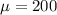
Calculate standard deviation

`\sigma = \sqrt{\mu (1 - p)`

`\sigma = \sqrt{200 * (1 - 0.50)`

`\sigma = \sqrt{200 * 0.50`

`\sigma = \sqrt{100`

`\sigma = 10`

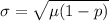
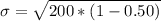
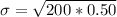
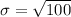
By continuity correction, we have:

`x \to x - 0.5`

`x \to 215 - 0.5`

`x \to 214.5`

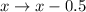
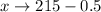
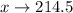
So, we have:

`P(x \ge 215) = P(x \ge 214.5)`

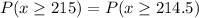
Calculating
`P(x \ge 214.5)`, we have:

`P(x \ge 214.5) = 1 - P(x < z)`

Calculate z score

`z = (x - \mu)/(\sigma)`

`z = (214.5 - 200)/(10)`

`z = (14.5)/(10)`

`z = 1.45`

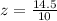
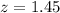
So, we have:

`P(x \ge 214.5) = 1 - P(x < 1.45)`

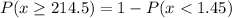
Using the z score probability table, we have:

`P(x < 1.45) = 0.92647`

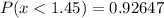
So, we have:

`P(x \ge 214.5) = 1 - 0.92647`

`P(x \ge 214.5) = 0.07353`