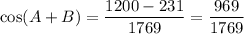Question

For positive acute angles A and B, it is known that cos A= 20/29 and tan B= 11/60. Find the value of cos(A + B) in simplest form.

Answer 1

`\displaystyle \cos(A + B) =(969)/(1769)`

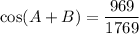
Explanation:

We are given that:

`\displaystyle \cos A=(20)/(29)\text{ and } \tan B=(11)/(60)`

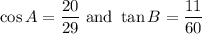
Where A and B are positive acute angles.

And we want to find cos(A + B).

Recall that cosine is the ratio of the adjacent side to the hypotenuse. Using this information, find the opposite side with respect to Angle A:

`o=√(29^2-20^2)=21`

Tangent is the ratio of the opposite side to the adjacent side. Find the hypotenuse with respect to Angle B:

`h=√(11^2+60^2)=61`

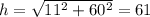
In summary:

With respect to Angle A, the adjacent side is 20, opposite is 21, and the hypotenuse is 29.

With respect to Angle B, the adjacent side is 60, the opposite is 11, and the hypotenuse is 61.

We can rewrite our expression as:

`\displaystyle \cos(A+B)=\cos A\cos B-\sin A\sin B`

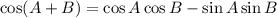
Using the above information, substitute in the appropriate values. Note that since A and B are positive acute angles, all trigonometric values will be positive. Hence:

`\displaystyle \cos(A + B)=\left((20)/(29)\right)\left((60)/(61)\right)-\left((21)/(29)\right)\left((11)/(61)\right)`

Simplify:

`\displaystyle \cos(A + B) =(1200-231)/(1769)=(969)/(1769)`