Question

At one moment during its flight a thrown basketball experiences a gravitational force of 1.5N down and air resistance of 0.40N(32 degree above horizontal). Calculate the magnitude and direction of of the net force of the ball

Answer 1

1. The magnitude of the net force is 1.33 N.

2. The direction is 14.8° with respect to the vertical.

Step-by-step explanation:

1. The magnitude of the net force is given by:

`|F| = \sqrt{F_(x)^(2) + F_(y)^(2)}`

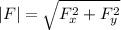
Where:

`F_(x)`: is the sum of the forces acting in the x-direction

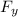`F_(y)`: is the sum of the forces acting in the y-direction

Let's find the forces acting in the x-direction and in the y-direction.

In the x-direction:

`\Sigma F_(x) = -F_(a)cos(\theta)`

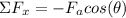
Where:

Fa: is the force of air resistance = -0.40 N. The negative sign is because this force is in the negative x-direction.

θ: is the angle = 32°

`\Sigma F_(x) = -0.40 N*cos(32) = -0.34 N`

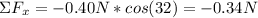
In the y-direction:

`\Sigma F_(y) = F_(g) + F_(a)sin(\theta)`

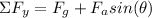
Where:

`F_(g)`: is the gravitational force = -1.5 N

`\Sigma F_(y) = -1.5 N + 0.40 N*sin(32) = -1.29 N`

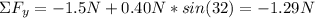
Hence, the magnitude of the net force is:

`|F| = \sqrt{(-0.34 N)^(2) + (-1.29)^(2)} = 1.33 N`

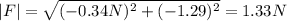
2. The direction of the net force is:

`tan(\alpha) = (F_(x))/(F_(y)) = (-0.34)/(-1.29)`

`\alpha = tan^(-1)((-0.34)/(-1.29)) = 14.8`

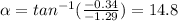
The angle is 14.8° with respect to the vertical.

I hope it helps you!