Answer:
A. Parallelogram
Explanation:
The given points are;
(-10, -4), (-7, -8), (-5, -4), (-2, -8)
Let 'A' represent the point (-10, -4), let 'B' represent the point (-7, -8), let 'C' represent the point (-5, -4), and let 'D' represent the point (-2, -8), we have;
The (horizontal) distance between points A and C = -5 - (-10) = 5
The (horizontal) distance between points B and D = -2 - (-7) = 5
Therefore;
The length of
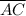 = The length of
= The length of
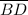
The length of
 = √((-10 - (-7))² + (-4 - (-8))²)) = 5
= √((-10 - (-7))² + (-4 - (-8))²)) = 5
The length of
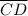 = √((-5 - (-2))² + (-4 - (-8))²)) = 5
= √((-5 - (-2))² + (-4 - (-8))²)) = 5
∴ The length of
 = The length of
= The length of
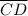
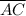 is parallel to the horizontal axis
is parallel to the horizontal axis
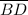 is parallel to the horizontal axis
is parallel to the horizontal axis
∴
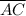 ║
║
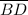
Given that
 =
=
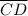 , then
, then
 ║
║
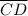
Therefore, the quadrilateral ABCD is a parallelogram
(The angle ∠ABD = 180 - arctan (4/3) ≈ 126.9 > 90, therefore, the parallelogram ABCD is not a rectangle.)