Answer:
The arc length and the area of the circle sector are approximately 9.076 inches and 58.992 square inches.
Explanation:
Geometrically speaking, we determine the arc length (
 ), in inches, and the area (
), in inches, and the area (
 ), in square inches, of a circle sector by means of these formulas:
), in square inches, of a circle sector by means of these formulas:
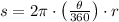 (1)
(1)
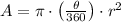 (2)
(2)
Where:
 - Radius, in inches.
- Radius, in inches.
 - Central angle, in sexagesimal degrees.
- Central angle, in sexagesimal degrees.
If we know that
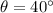 and
and
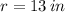 , then the arc length and the area of the circle sector are, respectively:
, then the arc length and the area of the circle sector are, respectively:
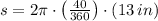
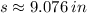
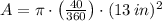
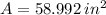
The arc length and the area of the circle sector are approximately 9.076 inches and 58.992 square inches.