Question

REINFORCE Tickets to the zoo cost $18 for adults and $8.25 for children. One day, the zoo sold 2,300 tickets and collected $30,168 in ticket sales. How many children and how many adults attended the zoo that day? Write a system and solve it by graphing. Be sure to sketch you graph, give the solution, and define your variables.

Answer 1

Given:

The cost of adults ticket = $18

The cost of children's ticket = $8.25

Total tickets = 2300

Total revenue = $30,168.

To find:

The number of children and number of adults attended the zoo that day.

Solution:

Let x be the number of children and y be the number of adults.

Equation for tickets:
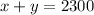`x+y=2300` ...(i)

Equation for revenue:
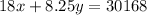`18x+8.25y=30168` ...(ii)

Plot the graphs of the given equations on a coordinate plane as shown below.

From the graph it is clear that the graph of both equations intersect each other at (1148,1152).

It means the number of adults is 1148 and the number of children is 1152.

It can be solved algebraically as shown below:

Substitute the value of y in (ii) from (i).

`18x+8.25(2300-x)=30168`

`18x+18975-8.25x=30168`

`9.75x=30168-18975`

`9.75x=11193`

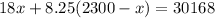
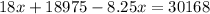
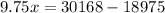
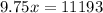
Divide both sides by 9.75.

`x=(11193)/(9.75)`

`x=1148`

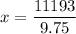
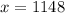
Putting
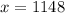`x=1148` in (i), we get

`1148+y=2300`

`y=2300-1148`

`y=1152`

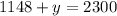
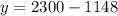
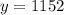
Therefore, the number of adults is 1148 and the number of children is 1152.