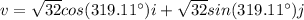Question

Give the trigonometric form of each vector (leave the magnitude as a square root) p=

(<2V6, -2V2)

Answer 1

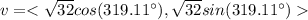`v=<√(32)cos(319.11^(\circ)),√(32)sin(319.11^(\circ))>` or
`v=√(32)cos(319.11^(\circ))i+√(32)sin(319.11^(\circ))j`

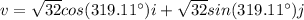
Explanation:

Find the magnitude of
`<2√(6),-2√(2)>`:

`||v||=\sqrt{(2√(6))^2+(-2√(2))^2}`

`||v||=√(24+8)`

`||v||=√(32)`

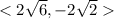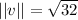
Find the direction angle of
`<2√(6),-2√(2)>`:

`\alpha=tan^(-1)|(-2√(2))/(2√(6))|`

`\alpha=tan^(-1)|-(√(3))/(2)|`

`\alpha=tan^(-1)((√(3))/(2))`

`\alpha=40.89^(\circ)`

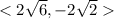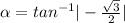
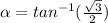
Since
`\alpha=40.89^(\circ)` is our reference angle, we determine our direction angle
`\theta` by verifying our angle is in Quadrant IV, which is where the vector is located. Therefore,
`\theta=360^(\circ)-\alpha=360^(\circ)-40.89^(\circ)=319.11^(\circ)`

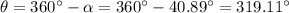
To represent a vector's magnitude and direction in trigonometric form, we use the form
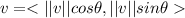`v=<||v||cos\theta,||v||sin\theta>` or
`v=||v||cos\theta i+||v||sin\theta j`.

In conclusion, the trigonometric form of the vector is:

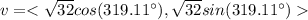`v=<√(32)cos(319.11^(\circ)),√(32)sin(319.11^(\circ))>` or

`v=√(32)cos(319.11^(\circ))i+√(32)sin(319.11^(\circ))j`